Background: CT examinations are commonly utilized for the diagnosis of internal diseases. The X-rays emitted during CT scans can elevate the risks of developing solid cancers by causing DNA damage. The risk of CT scan-induced solid cancers is intricately linked to the organ doses specific to each patient. The Support Vector Regression (SVR) algorithm exhibits the capability to swiftly and accurately predict organ doses. Kernel functions, including linear, polynomial, and radial basis (RBF) functions, play a crucial role in the overall performance of SVR when predicting patient-specific organ doses from CT scans. Therefore, it is imperative to investigate the influence of kernel selection on the comprehensive predictive effectiveness of SVR. Purpose: This study investigates the impact of kernel functions on the predictive performance of SVR models trained by radiomics features, and to pinpoint the optimal kernel function for predicting patient-specific organ doses from CT scans. Methods: CT images from head and abdominal CT scans were processed using DeepViewer®, an auto-segmentation tool for defining regions of interest (ROIs) within their organs. Radiomics features were extracted from the CT data and ROIs. Benchmark organ doses were calculated through Monte Carlo simulations. SVR models, utilizing the radiomics features, were trained with linear-, polynomial-, and RBF kernels to predict patient-specific organ doses from CT scans. The robustness of the SVR prediction was examined by applying 25 random sample splits with each kernel. The mean absolute percentage error (MAPE) and coefficient of determination (R2) were compared among the kernels to identify the optimal kernel. Results: The linear kernel obtains better overall predictive performance than the polynomial and RBF kernels. The SVR trained with the linear kernel function achieves lower MAPE values, below 5% for head organs and under 6.8% for abdominal organs. Furthermore, it shows higher R2 values exceeding 0.85 for head organs and going beyond 0.8 for abdominal organs. Conclusions: Kernel selection severely impact the overall performance of SVR models. The optimal kernel varies with CT scanned parts and organ types indicating the necessity to conduct organ-specific kernel selection.
| Published in | Radiation Science and Technology (Volume 11, Issue 1) |
| DOI | 10.11648/j.rst.20251101.11 |
| Page(s) | 1-11 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2025. Published by Science Publishing Group |
CT, Organ Dose, SVR, Radiomics Features, Kernel Function
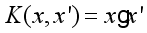 (3)
(3) 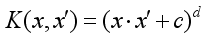 (4)
(4) 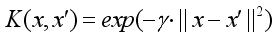 (5)
(5) SVR | Support Vector Regression |
MAPE | Mean Absolute Percentage Error |
R2 | R-squared |
RBF | Radial Basis Function |
IQR | Interquartile Range |
ROI | Regions of Interest |
| [1] | Hussain, S., Mubeen, I., Ullah, N., Shah, S. S. U. D., Khan, B. A., Zahoor, M., Ullah, R., Khan, F. A. and Sultan, M. A., 2022. Modern Diagnostic Imaging Technique Applications and Risk Factors in the Medical Field: A Review. BioMed research international, 2022, p. 5164970. |
| [2] | Abhisheka, B., Biswas, S. K., Purkayastha, B., Das, D. and Escargueil, A., 2023. Recent trend in medical imaging modalities and their applications in disease diagnosis: a review. Multimedia Tools and Applications, pp. 1-36. |
| [3] | Yitbarek, D. and Dagnaw, G. G., 2022. Application of advanced imaging modalities in veterinary medicine: a review. Veterinary Medicine: Research and Reports, pp. 117-125. |
| [4] | Furlani, M., Riberti, N., Gatto, M. L. and Giuliani, A., 2023. High-Resolution Phase-Contrast Tomography on Human Collagenous Tissues: A Comprehensive Review. Tomography, 9(6), pp. 2116-2133. |
| [5] | Spinnato, P., Patel, D. B., Di Carlo, M., Bartoloni, A., Cevolani, L., Matcuk, G. R. and Crombé, A., 2022. Imaging of Musculoskeletal Soft-Tissue Infections in Clinical Practice: A Comprehensive Updated Review. Microorganisms, 10(12), p. 2329. |
| [6] | Addala, D. N., Denniston, P., Sundaralingam, A. and Rahman, N. M., 2023. Optimal diagnostic strategies for pleural diseases and identifying high-risk patients. Expert Review of Respiratory Medicine, 17(1), pp. 15-26. |
| [7] | Hines Jr, J. J., Mikhitarian, M. A., Patel, R. and Choy, A., 2021. Spectrum and relevance of incidental bowel findings on computed tomography. Radiologic Clinics, 59(4), pp. 647-660. |
| [8] | Jain, S., 2021. Radiation in medical practice & health effects of radiation: Rationale, risks, and rewards. Journal of Family Medicine and Primary Care, 10(4), p. 1520. |
| [9] | Shao, Y. H., Tsai, K., Kim, S., Wu, Y. J. and Demissie, K., 2020. Exposure to tomographic scans and cancer risks. JNCI cancer spectrum, 4(1), p. pkz072. |
| [10] | Foucault, A., Ancelet, S., Dreuil, S., Caer-Lorho, S., Ducou Le Pointe, H., Brisse, H., Chateil, J. F., Lee, C., Leuraud, K. and Bernier, M. O., 2022. Childhood cancer risks estimates following CT scans: an update of the French CT cohort study. European Radiology, 32(8), pp. 5491-5498. |
| [11] | Farkouh, A. A. and Baldwin, D. D., 2023. Radiation Hazards in Endourology. In Percutaneous Renal Surgery (pp. 121-141). Cham: Springer International Publishing. |
| [12] | Maier, J., Eulig, E., Dorn, S., Sawall, S. and Kachelrieß, M., 2018, November. Real-time patient-specific CT dose estimation using a deep convolutional neural network. In 2018 IEEE Nuclear Science Symposium and Medical Imaging Conference Proceedings (NSS/MIC) (pp. 1-3). IEEE. |
| [13] | Xie, T. and Zaidi, H., 2019. Estimation of the radiation dose in pregnancy: an automated patient-specific model using convolutional neural networks. European radiology, 29, pp. 6805-6815. |
| [14] | Imran, A. A. Z., Wang, S., Pal, D., Dutta, S., Patel, B., Zucker, E. and Wang, A., 2021. Personalized CT organ dose estimation from scout images. In Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, September 27–October 1, 2021, Proceedings, Part IV 24 (pp. 488-498). Springer International Publishing. |
| [15] | Tzanis E, Damilakis J. A novel methodology to train and deploy a machine learning model for patient-specific dose assessment in head CT. Eur Radiol. 2022; 32(9): 6418-6426. |
| [16] | Christner, J. A., Braun, N. N., Jacobsen, M. C., Carter, R. E., Kofler, J. M. and McCollough, C. H., 2012. Size-specific dose estimates for adult patients at CT of the torso. Radiology, 265(3), pp. 841-847. |
| [17] | Moore, B. M., Brady, S. L., Mirro, A. E. and Kaufman, R. A., 2014. Size‐specific dose estimate (SSDE) provides a simple method to calculate organ dose for pediatric CT examinations. Medical physics, 41(7), p. 071917. |
| [18] | Franck, C., Vandevoorde, C., Goethals, I., Smeets, P., Achten, E., Verstraete, K., Thierens, H. and Bacher, K., 2016. The role of Size-Specific Dose Estimate (SSDE) in patient-specific organ dose and cancer risk estimation in paediatric chest and abdominopelvic CT examinations. European radiology, 26, pp. 2646-2655. |
| [19] | Brink, J. A. and Morin, R. L., 2012. Size-specific dose estimation for CT: how should it be used and what does it mean?. Radiology, 265(3), pp. 666-668. |
| [20] | Maior, C. B., Santana, J. M., Lins, I. D. and Moura, M. J., 2021. Convolutional neural network model based on radiological images to support COVID-19 diagnosis: Evaluating database biases. Plos one, 16(3), p. e0247839. |
| [21] | Park, D. J., Park, M. W., Lee, H., Kim, Y. J., Kim, Y. and Park, Y. H., 2021. Development of machine learning model for diagnostic disease prediction based on laboratory tests. Scientific reports, 11(1), p. 7567. |
| [22] | Jeyaraman, M., Balaji, S., Jeyaraman, N. and Yadav, S., 2023. Unraveling the ethical enigma: Artificial intelligence in healthcare. Cureus, 15(8). |
| [23] | Murphy, K., Di Ruggiero, E., Upshur, R., Willison, D. J., Malhotra, N., Cai, J. C., Malhotra, N., Lui, V. and Gibson, J., 2021. Artificial intelligence for good health: a scoping review of the ethics literature. BMC medical ethics, 22(1), pp. 1-17. |
| [24] | Drucker, H., Burges, C. J., Kaufman, L., Smola, A., & Vapnik, V. N. (1996). Support Vector Regression Machines. Neural Information Processing Systems. |
| [25] | Chih-Cheng Yang, Wan-Jui Lee and Shie-Jue Lee, "Learning of Kernel Functions in Support Vector Machines," The 2006 IEEE International Joint Conference on Neural Network Proceedings, Vancouver, BC, Canada, 2006, pp. 1150-1155, |
| [26] |
Shao W, Xin L, Yi Y, Huang Y, Qu L, Zhuo W, Liu H. Fast prediction of patient-specific organ doses in brain CT scans using support vector regression algorithm. Phys Med Biol. 2023 Dec 12.
https://doi.org/10.1088/1361-6560/ad14c7 Epub ahead of print. |
| [27] | Peng Z, Chang YK, Song YC, et al. Validation and Clinical Application of DL-Based Automatic Target and OAR Segmentation Software, DeepViewer. In: Proceedings of the American Association of Physicists in Medicine Annual Meeting (Vancouver, BC, July 12-16). 2020: 123-124. |
| [28] | Thomas Phil, Thomas Albrecht, Skylar Gay, & Mathis Ersted Rasmussen. (2023). Sikerdebaard/dcmrtstruct2nii: dcmrtstruct2nii v5 (Version v5). Zenodo. Available from: |
| [29] | van Griethuysen JJM et al. Computational radiomics system to decode the radiographic phenotype. Cancer Res 2017; 77: e104-e107. |
| [30] | Rebuffi S-A, Gowal S, Calian DA, et al. Data Augmentation Can Improve Robustness. In: Advances in Neural Information Processing Systems 34 (NeurIPS 2021). Neural Information Processing Systems Foundation; 2021: 1234-1245. |
| [31] | Zhang, J. and Wang, X., 1997. Selecting the best regression equation via the P-value of F-test. Metrika, 46, pp. 33-40. |
| [32] |
Anaconda | The World’s Most Popular Data Science Platform.
https://www.anaconda.com/ Accessed January 28, 2022. |
| [33] | Bert J et al. GGEMS: GPU GEant4-based Monte Carlo Simulation platform. In: Proceedings of the IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC). IEEE; 2016: 1234-1245. |
APA Style
Shao, W., Lin, X., Huang, Y., Qu, L., Zhuo, W., et al. (2025). Effect of Kernel Functions on the Performance of Support Vector Regression Algorithm in Predicting Patient-Specific Organ Doses from CT Scans. Radiation Science and Technology, 11(1), 1-11. https://doi.org/10.11648/j.rst.20251101.11
ACS Style
Shao, W.; Lin, X.; Huang, Y.; Qu, L.; Zhuo, W., et al. Effect of Kernel Functions on the Performance of Support Vector Regression Algorithm in Predicting Patient-Specific Organ Doses from CT Scans. Radiat. Sci. Technol. 2025, 11(1), 1-11. doi: 10.11648/j.rst.20251101.11
AMA Style
Shao W, Lin X, Huang Y, Qu L, Zhuo W, et al. Effect of Kernel Functions on the Performance of Support Vector Regression Algorithm in Predicting Patient-Specific Organ Doses from CT Scans. Radiat Sci Technol. 2025;11(1):1-11. doi: 10.11648/j.rst.20251101.11
@article{10.11648/j.rst.20251101.11,
author = {Wencheng Shao and Xin Lin and Ying Huang and Liangyong Qu and Weihai Zhuo and Haikuan Liu},
title = {Effect of Kernel Functions on the Performance of Support Vector Regression Algorithm in Predicting Patient-Specific Organ Doses from CT Scans
},
journal = {Radiation Science and Technology},
volume = {11},
number = {1},
pages = {1-11},
doi = {10.11648/j.rst.20251101.11},
url = {https://doi.org/10.11648/j.rst.20251101.11},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.rst.20251101.11},
abstract = {Background: CT examinations are commonly utilized for the diagnosis of internal diseases. The X-rays emitted during CT scans can elevate the risks of developing solid cancers by causing DNA damage. The risk of CT scan-induced solid cancers is intricately linked to the organ doses specific to each patient. The Support Vector Regression (SVR) algorithm exhibits the capability to swiftly and accurately predict organ doses. Kernel functions, including linear, polynomial, and radial basis (RBF) functions, play a crucial role in the overall performance of SVR when predicting patient-specific organ doses from CT scans. Therefore, it is imperative to investigate the influence of kernel selection on the comprehensive predictive effectiveness of SVR. Purpose: This study investigates the impact of kernel functions on the predictive performance of SVR models trained by radiomics features, and to pinpoint the optimal kernel function for predicting patient-specific organ doses from CT scans. Methods: CT images from head and abdominal CT scans were processed using DeepViewer®, an auto-segmentation tool for defining regions of interest (ROIs) within their organs. Radiomics features were extracted from the CT data and ROIs. Benchmark organ doses were calculated through Monte Carlo simulations. SVR models, utilizing the radiomics features, were trained with linear-, polynomial-, and RBF kernels to predict patient-specific organ doses from CT scans. The robustness of the SVR prediction was examined by applying 25 random sample splits with each kernel. The mean absolute percentage error (MAPE) and coefficient of determination (R2) were compared among the kernels to identify the optimal kernel. Results: The linear kernel obtains better overall predictive performance than the polynomial and RBF kernels. The SVR trained with the linear kernel function achieves lower MAPE values, below 5% for head organs and under 6.8% for abdominal organs. Furthermore, it shows higher R2 values exceeding 0.85 for head organs and going beyond 0.8 for abdominal organs. Conclusions: Kernel selection severely impact the overall performance of SVR models. The optimal kernel varies with CT scanned parts and organ types indicating the necessity to conduct organ-specific kernel selection.
},
year = {2025}
}
TY - JOUR T1 - Effect of Kernel Functions on the Performance of Support Vector Regression Algorithm in Predicting Patient-Specific Organ Doses from CT Scans AU - Wencheng Shao AU - Xin Lin AU - Ying Huang AU - Liangyong Qu AU - Weihai Zhuo AU - Haikuan Liu Y1 - 2025/03/21 PY - 2025 N1 - https://doi.org/10.11648/j.rst.20251101.11 DO - 10.11648/j.rst.20251101.11 T2 - Radiation Science and Technology JF - Radiation Science and Technology JO - Radiation Science and Technology SP - 1 EP - 11 PB - Science Publishing Group SN - 2575-5943 UR - https://doi.org/10.11648/j.rst.20251101.11 AB - Background: CT examinations are commonly utilized for the diagnosis of internal diseases. The X-rays emitted during CT scans can elevate the risks of developing solid cancers by causing DNA damage. The risk of CT scan-induced solid cancers is intricately linked to the organ doses specific to each patient. The Support Vector Regression (SVR) algorithm exhibits the capability to swiftly and accurately predict organ doses. Kernel functions, including linear, polynomial, and radial basis (RBF) functions, play a crucial role in the overall performance of SVR when predicting patient-specific organ doses from CT scans. Therefore, it is imperative to investigate the influence of kernel selection on the comprehensive predictive effectiveness of SVR. Purpose: This study investigates the impact of kernel functions on the predictive performance of SVR models trained by radiomics features, and to pinpoint the optimal kernel function for predicting patient-specific organ doses from CT scans. Methods: CT images from head and abdominal CT scans were processed using DeepViewer®, an auto-segmentation tool for defining regions of interest (ROIs) within their organs. Radiomics features were extracted from the CT data and ROIs. Benchmark organ doses were calculated through Monte Carlo simulations. SVR models, utilizing the radiomics features, were trained with linear-, polynomial-, and RBF kernels to predict patient-specific organ doses from CT scans. The robustness of the SVR prediction was examined by applying 25 random sample splits with each kernel. The mean absolute percentage error (MAPE) and coefficient of determination (R2) were compared among the kernels to identify the optimal kernel. Results: The linear kernel obtains better overall predictive performance than the polynomial and RBF kernels. The SVR trained with the linear kernel function achieves lower MAPE values, below 5% for head organs and under 6.8% for abdominal organs. Furthermore, it shows higher R2 values exceeding 0.85 for head organs and going beyond 0.8 for abdominal organs. Conclusions: Kernel selection severely impact the overall performance of SVR models. The optimal kernel varies with CT scanned parts and organ types indicating the necessity to conduct organ-specific kernel selection. VL - 11 IS - 1 ER -